The CBC padding oracle attack demonstrates how what might initially seem like a small issue can balloon into a devastating attack that can result in total reconstruction of the plaintext by the attacker. It’s also one of the harder challenges in Set 3 of Cryptopals.
The problem
It goes like this: an attacker has access to an oracle that will take a ciphertext (i.e. what we need to decrypt) and return a boolean indicating whether or not the padding was valid. My padding oracle function looked like this:
def cbc_padding_oracle(key: bytes, ciphertext: bytes, iv: bytes) -> bool:
try:
aes_cbc_decrypt(key, ciphertext, iv, remove_padding=True)
return True
except BadPaddingValidation:
return Falsewhere BadPaddingValidation was a custom exception indicating that - you guessed it - the padding was invalid.
The following (16-byte) block has valid padding:

and our oracle will tell us that. This means that we learn something about the plaintext.
From this fact alone, we can decrypt the ciphertext.
How it works
Looking at how CBC decryption works, we can figure out how to use this fact to get the plaintext:
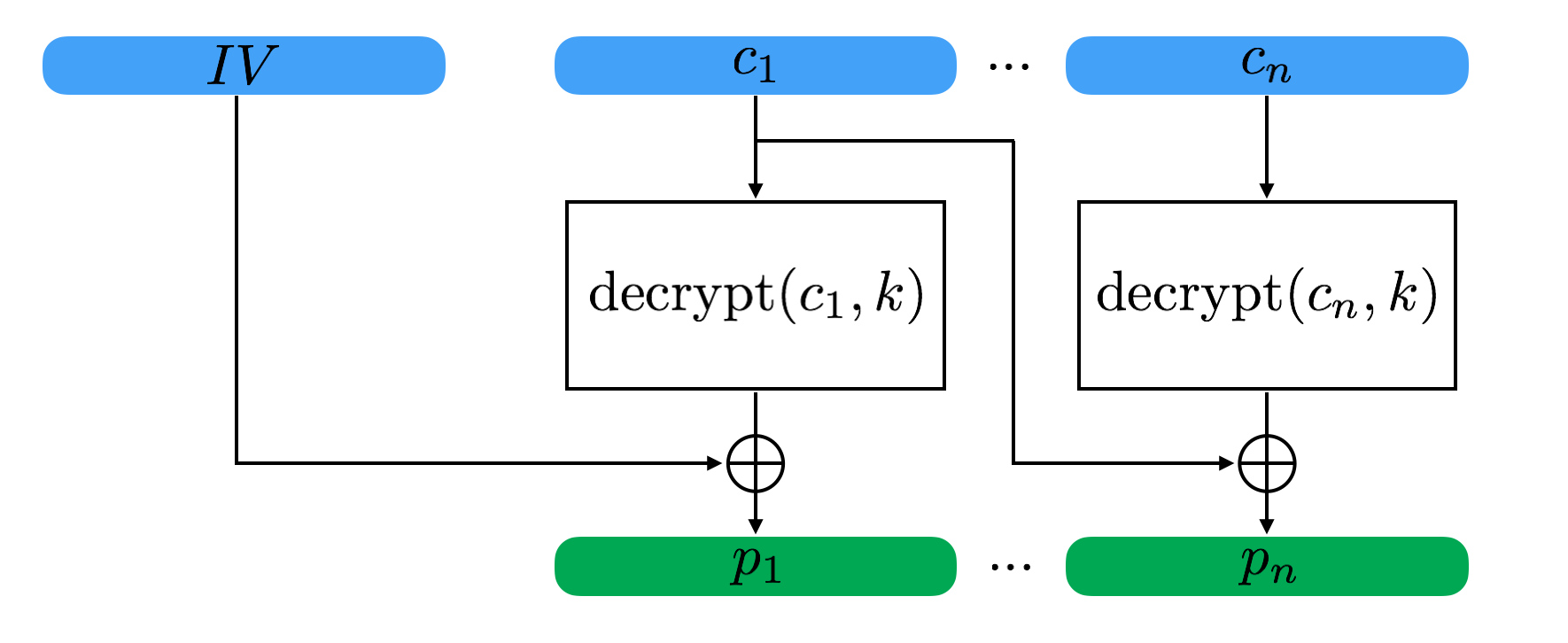
Well, we don’t know the IV so let’s ignore that. We do have all the ciphertext blocks. And we can learn if the final N bytes of any given plaintext are valid via our oracle.
Looking at the diagram we can see that:
$c_{n-1} \oplus \mbox{decrypt}(c_n, k) = p_n$
As the attacker, we’ll copy $c_{n-1}$ to a test block we’ll call $t$ and introduce a single bit change in the final byte:
$t \oplus \mbox{decrypt}(c_n, k) = p_n$
We’ll keep introducing single bit changes in the final byte until we get a valid response from the oracle. Then we’ve learned:
$t[15] \oplus \mbox{decrypt}(c_n, k)[15] = 01$
Rearranging:
$\mbox{decrypt}(c_n, k)[15] = 01 \oplus t[15]$
Meaning that we learned about the final byte of the block cipher decryption output which we can reuse now with $c_{n-1}$ and $c_n$ to get the real final byte of plaintext:
$p_n[15] = c_{n-1}[15] \oplus \mbox{decrypt}(c_n, k)[15]$
That’s the first byte reconstructed.
Let’s go
Starting at the rightmost block, we can move right to left decrypting each plaintext byte.
For bytes that aren’t the final byte in the block, we can use what we learned so far in the block to compute what the valid padding bytes would be for the bytes right of the target byte. For example, for the second-to-last byte, we are looking for padding that validates to:

We can compute the final byte of our test ciphertext such that it will equal our desired padding byte value 02:
$t[15] = \mbox{decrypt}(c_n, k)[15] \oplus 02$
So as we decrypt each block we just need to keep track of the output of the block cipher prior to the xor so we can compute this.
One gotcha
I got the above working pretty quickly, but realized my attack was not working reliably. Occasionally, I guessed the wrong answer early on in the plaintext reconstruction. Debugging I discovered the following case when reconstructing the first byte:
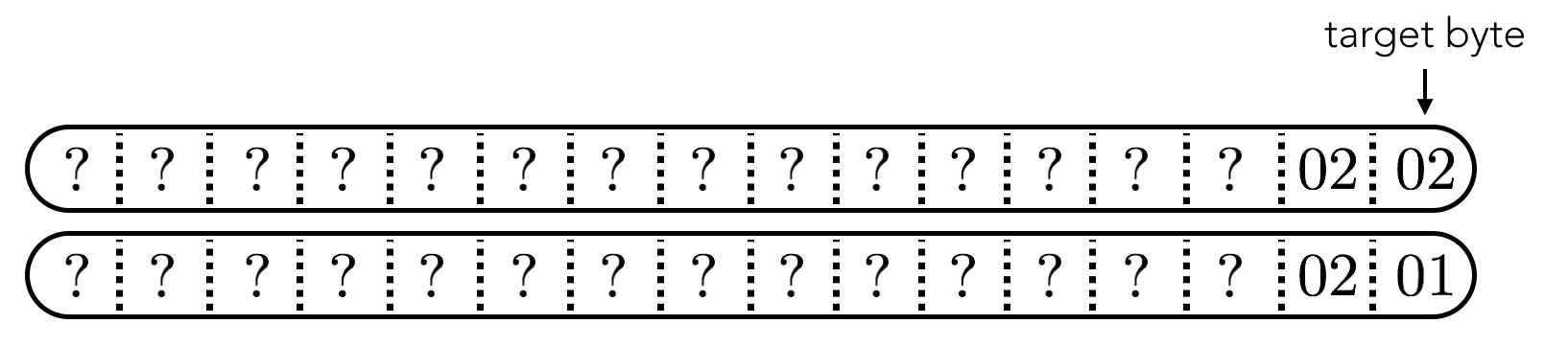
There can be multiple “correct” answers for a given byte, i.e. there can be multiple ciphertexts that will have valid padding. Here in the example we have two valid ciphertexts when computing the last byte in the ciphertext: one with 01 in the final byte position (what we’re looking for) and one where the second-to-last byte is 02 and produces a valid padding result (not what we’re looking for).
To handle this case, before settling on a given byte, I’d first modify the byte before the target byte and check if the padding was still valid:
byte_num_to_edit = self.block_size + byte_num - 2
degeneracy_ciphertext = flip_nth_bit(
full_test_ciphertext, byte_num_to_edit - self.block_size
)
if cbc_padding_oracle(self.key, degeneracy_ciphertext, self.iv):
pass
else:
continueThis enabled me to distinguish between the two above cases, and ensure that there was only a single, correct answer for each byte.
My solution is here.